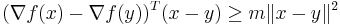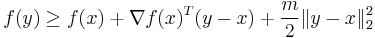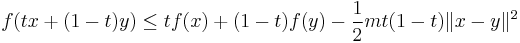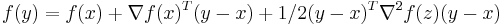Convex function
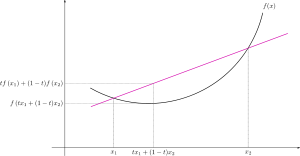

In mathematics, a real-valued function  defined on an interval (or on any convex subset of some vector space) is called convex, concave upwards, concave up or convex cup, if for any two points
defined on an interval (or on any convex subset of some vector space) is called convex, concave upwards, concave up or convex cup, if for any two points  and
and  in its domain X and any
in its domain X and any ![t\in[0,1]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/d9a06fde4663cdd5b1ba693e9127232f.png) ,
,
A function is called strictly convex if
for any t in (0, 1) and 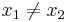 .
.
A function ƒ is said to be concave if −ƒ is convex.
Pictorially, a function is called 'convex' if the function lies below or on the straight line segment connecting two points, for any two points in the interval.
Sometimes an alternative definition is used:
- A function is convex if its epigraph (the set of points lying on or above the graph) is a convex set.
These two definitions are equivalent, i.e., one holds if and only if the other one is true.
Contents |
Properties
Suppose ƒ is a one variable function defined on an interval, and let
(note that R(x,y) is the slope of the red line in the above drawing; note also that the function R is symmetric in x,y). ƒ is convex if and only if R(x,y) is monotonically non-decreasing in x, for y fixed (or viceversa). This characterization of convexity is quite useful to prove the following results.
A convex function ƒ defined on some open interval C is continuous on C and Lipschitz continuous on any closed subinterval. ƒ admits left and right derivatives, and these are monotonically non-decreasing. As a consequence, ƒ is differentiable at all but at most countably many points. If C is closed, then ƒ may fail to be continuous at the endpoints of C (an example is shown in the examples' section).
A function is midpoint convex on an interval C if
for all x and y in C. This condition is only slightly weaker than convexity. For example, a real valued Lebesgue measurable function that is midpoint convex will be convex.[1] In particular, a continuous function that is midpoint convex will be convex.
A differentiable function of one variable is convex on an interval if and only if its derivative is monotonically non-decreasing on that interval. If a function is differentiable and convex then it is also continuously differentiable.
A continuously differentiable function of one variable is convex on an interval if and only if the function lies above all of its tangents:
for all x and y in the interval. In particular, if ƒ '(c) = 0, then c is a global minimum of ƒ(x).
A twice differentiable function of one variable is convex on an interval if and only if its second derivative is non-negative there; this gives a practical test for convexity. If its second derivative is positive then it is strictly convex, but the converse does not hold. For example, the second derivative of ƒ(x) = x4 is ƒ "(x) = 12 x2, which is zero for x = 0, but x4 is strictly convex.
More generally, a continuous, twice differentiable function of several variables is convex on a convex set if and only if its Hessian matrix is positive semidefinite on the interior of the convex set.
Any local minimum of a convex function is also a global minimum. A strictly convex function will have at most one global minimum.
For a convex function ƒ, the sublevel sets {x | ƒ(x) < a} and {x | ƒ(x) ≤ a} with a ∈ R are convex sets. However, a function whose sublevel sets are convex sets may fail to be a convex function. A function whose sublevel sets are convex is called a quasiconvex function.
Jensen's inequality applies to every convex function ƒ. If X is a random variable taking values in the domain of ƒ, then 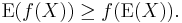 (Here
(Here 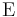 denotes the mathematical expectation.)
denotes the mathematical expectation.)
Convex function calculus
- If
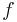 and
and  are convex functions, then so are
are convex functions, then so are 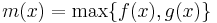 and
and 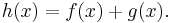
- If
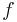 and
and  are convex functions and if
are convex functions and if  is non-decreasing, then
is non-decreasing, then 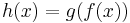 is convex.
is convex. - Convexity is invariant under affine maps: that is, if
 is convex with
is convex with 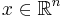 , then so is
, then so is 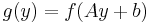 with
with 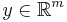 , where
, where 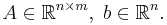
- If
 is convex in
is convex in 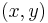 and
and  is a convex nonempty set, then
is a convex nonempty set, then 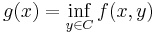 is convex in
is convex in 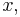 provided
provided 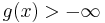 for some
for some 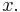
- If
 is convex, then its perspective function
is convex, then its perspective function 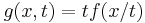 (whose domain is
(whose domain is 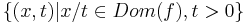 ) is convex.
) is convex.
Strongly convex functions
The concept of strong convexity extends the notion of strict convexity. A strongly convex function is also strictly convex, but not vice-versa. A differentiable function f is called strongly convex with parameter m > 0 if the following equation holds for all points x,y in its domain:
This is equivalent to the following
It is not necessary for a function to be differentiable in order to be strongly convex. A third definition for a strongly convex function, with parameter m, is that, for all x,y in the domain and ![t\in [0,1]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/d9a06fde4663cdd5b1ba693e9127232f.png) ,
,
(given that 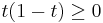 for
for ![t\in[0,1]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/d9a06fde4663cdd5b1ba693e9127232f.png) .)
.)
If the function f is twice continuously differentiable, then f is strongly convex with parameter m if and only if 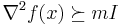 for all x in the domain, where I is the identity and
for all x in the domain, where I is the identity and 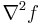 is the Hessian matrix, and the inequality
is the Hessian matrix, and the inequality 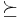 means that
means that 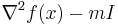 is positive definite. This is equivalent to requiring that the minimum eigenvalue of
is positive definite. This is equivalent to requiring that the minimum eigenvalue of 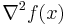 be at least m for all x. If the domain is just the real line, then
be at least m for all x. If the domain is just the real line, then 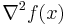 is just the second derivative
is just the second derivative 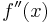 , so the condition becomes
, so the condition becomes 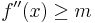 . If m = 0, then this means the Hessian is positive semidefinite (or if the domain is the real line, it means that
. If m = 0, then this means the Hessian is positive semidefinite (or if the domain is the real line, it means that 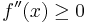 ), which implies the function is convex, and perhaps strictly convex, but not strongly convex.
), which implies the function is convex, and perhaps strictly convex, but not strongly convex.
Assuming still that the function is twice continuously differentiable, we show that the lower bound of 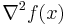 implies that it is strongly convex. Start by using Taylor's Theorem:
implies that it is strongly convex. Start by using Taylor's Theorem:
for some (unknown) ![z \in [x,y]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/9636997189f4b390a6c31678a5293b03.png) . Then
. Then 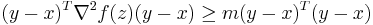 by the assumption about the eigenvalues, and hence we recover the second strong convexity equation above.
by the assumption about the eigenvalues, and hence we recover the second strong convexity equation above.
The distinction between convex, strictly convex, and strongly convex can be subtle at first glimpse. If 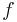 is twice continuously differentiable and the domain is the real line, then we can characterize it as follows:
is twice continuously differentiable and the domain is the real line, then we can characterize it as follows:
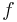 convex if and only if
convex if and only if 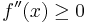 for all
for all 
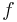 strictly convex if
strictly convex if 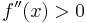 for all
for all  (note: this is necessary, but not sufficient)
(note: this is necessary, but not sufficient) strongly convex if and only if
strongly convex if and only if 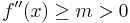 for all
for all 
For example, consider a function 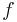 that is strictly convex, and suppose there is a sequence of points
that is strictly convex, and suppose there is a sequence of points 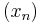 such that
such that 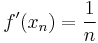 . Even though
. Even though 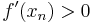 , the function is not strongly convex because
, the function is not strongly convex because 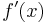 will become arbitrarily small.
will become arbitrarily small.
Strongly convex functions are in general easier to work with than convex or strictly convex functions, since they are a smaller class. Like strictly convex functions, strongly convex functions have unique minima.
Examples
- The function
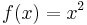 has
has  at all points, so ƒ is a convex function. It is also strongly convex (and hence strictly convex too), with strong convexity constant 2.
at all points, so ƒ is a convex function. It is also strongly convex (and hence strictly convex too), with strong convexity constant 2. - The function
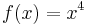 has
has 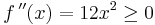 , so ƒ is a convex function. It is strictly convex, even though the second derivative is not strictly positive at all points. It is not strongly convex.
, so ƒ is a convex function. It is strictly convex, even though the second derivative is not strictly positive at all points. It is not strongly convex. - The absolute value function
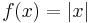 is convex, even though it does not have a derivative at the point x = 0. It is not strictly convex.
is convex, even though it does not have a derivative at the point x = 0. It is not strictly convex. - The function
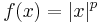 for 1 ≤ p is convex.
for 1 ≤ p is convex. - The exponential function
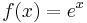 is convex. It is also strictly convex, since
is convex. It is also strictly convex, since 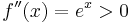 , but it is not strongly convex since the second derivative can be arbitrarily close to zero. More generally, the function
, but it is not strongly convex since the second derivative can be arbitrarily close to zero. More generally, the function 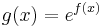 is logarithmically convex if ƒ is a convex function.
is logarithmically convex if ƒ is a convex function. - The function ƒ with domain [0,1] defined by ƒ(0) = ƒ(1) = 1, ƒ(x) = 0 for 0 < x < 1 is convex; it is continuous on the open interval (0, 1), but not continuous at 0 and 1.
- The function x3 has second derivative 6x; thus it is convex on the set where x ≥ 0 and concave on the set where x ≤ 0.
- Every linear transformation taking values in
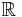 is convex but not strictly convex, since if f is linear, then
is convex but not strictly convex, since if f is linear, then 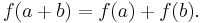 This statement also holds if we replace "convex" by "concave".
This statement also holds if we replace "convex" by "concave". - Every affine function taking values in
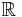 , i.e., each function of the form
, i.e., each function of the form 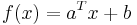 , is simultaneously convex and concave.
, is simultaneously convex and concave. - Every norm is a convex function, by the triangle inequality.
- If ƒ is convex, the perspective function
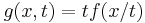 is convex for t > 0.
is convex for t > 0. - Examples of functions that are monotonically increasing but not convex include
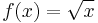 and g(x) = log(x).
and g(x) = log(x). - Examples of functions that are convex but not monotonically increasing include
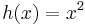 and
and 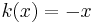 .
. - The function ƒ(x) = 1/x2, with f(0) = +∞, is convex on the interval (0, +∞) and convex on the interval (-∞,0), but not convex on the interval (-∞, +∞), because of the singularity at x = 0.
See also
- Concave function
- Convex optimization
- Geodesic convexity
- Kachurovskii's theorem, which relates convexity to monotonicity of the derivative
- Logarithmically convex function
- Quasiconvex function
- Subderivative of a convex function
- Jensen's inequality
- Hermite–Hadamard inequality
References
- Bertsekas, Dimitri (2003). Convex Analysis and Optimization. Athena Scientific.
- Borwein, Jonathan, and Lewis, Adrian. (2000). Convex Analysis and Nonlinear Optimization. Springer.
- Donoghue, William F. (1969). Distributions and Fourier Transforms. Academic Press.
- Hiriart-Urruty, Jean-Baptiste, and Lemaréchal, Claude. (2004). Fundamentals of Convex analysis. Berlin: Springer.
- Krasnosel'skii M.A., Rutickii Ya.B. (1961). Convex Functions and Orlicz Spaces. Groningen: P.Noordhoff Ltd.
- Luenberger, David (1984). Linear and Nonlinear Programming. Addison-Wesley.
- Luenberger, David (1969). Optimization by Vector Space Methods. Wiley & Sons.
- Rockafellar, R. T. (1970). Convex analysis. Princeton: Princeton University Press.
- Thomson, Brian (1994). Symmetric Properties of Real Functions. CRC Press.
External links
- Stephen Boyd and Lieven Vandenberghe, Convex Optimization (PDF)
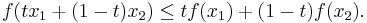
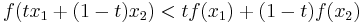
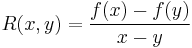
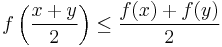
![f(x) \geq f(y) + f'(y)[x-y]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/bcdde26e590e46cd177693d64fc25fe8.png)